Überlegungen zu Weichenfiltern

Entwurfsziel für Weichenfilter

Der Entwurf eines Weichenfilters hat zum Ziel ein Frequenzgemisch in einzelne Kanäle aufzuteilen, diese dann zu bearbeiten und schließlich die entstandenen Teilsignale wieder so zusammenzufügen, dass deren Summe wieder dem ursprünglichen Signal entspricht. Die erfolgte Aufteilung und Zusammenfügung kann dann am Ergebnis nicht mehr erkannt werden.

Wenn man das für ein Weichenfilter für Lautsprecher übersetzt, dann ist man mit der Tatsache konfrontiert, dass ein Töner nur etwa ein bis zwei Frequenzdekaden betrags- und phasenrichtig in Schalldruck wandeln kann, man also die 3 Frequenzdekaden von 16 Hz bis 16 kHz in mehrere Frequenzbereiche aufspalten muss, um sicherzustellen, dass die Addition zum Summenschalldruck weitgehend ideal erfolgt. Dabei wird vorausgesetzt, dass die einzelnen Töner das zugewiesene Frequenzband und dessen nähere Umgebung betrags- und phasenrichtig in Schalldruck übersetzten, was im Allgemeinen nur mit gegengekoppelten Tönern möglich ist, die den Weg, die Geschwindigkeit, oder die Beschleunigung der Membran messen und über einen Vergleich mit dem elektrischen Eingangssignal regeln.

Unter der oben genannten Annahme, dass Töner für einzelne Frequenzbereiche das elektrische Signal weitgehend ideal in Schalldruck übersetzten, folgt daraus für Weichenfilter in der Laplace-Notation mit der komplexen Kreisfrequenz p:

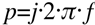
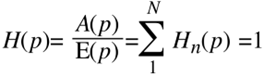
Die Übertragungsfunktion H(p), welche die Übertragung des Eingangssignals E(p) zum Ausgangssignal A(p) beschreibt und in eine Summe von N einzelnen Teilübertragungsfunktionen zerlegt wird, muss den Wert Eins haben. Dann und nur dann addieren sich die Ausgangssignale der N Teilübertragungsfunktionen wieder zum ursprünglichen Signal.

Veranschaulicht man sich das für zwei Wege, also einen Tiefpasskanal und einen Hochpasskanal, so muss offensichtlich gelten:

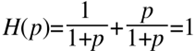
Die Summe aus der Tiefpassübertragungsfunktion (erster Summand) und der Hochpassübertragungsfunktion (zweiter Summand) ergibt Eins. Somit ist das Ausgangssignal nach der Summierung gleich dem Eingangssignal (siehe Definition von H(p)).

In der Realität müssen weitere Randbedingungen beachtet werden: Die im Beispiel verwendete Tiefpassfunktion ist vom Grad 1 (p kommt nur in der ersten Potenz vor) und hat somit einen Amplitudenfrequenzgang von 20 dB/Dekade. Das bedeutet einen Signalanstieg, oder -abfall um den Faktor 10 entsprechend 20 dB je Frequenzdekade. Trennt man z.B. das gesamte Hörfrequenzband logarithmisch äquidistant in drei Frequenzbänder auf, also von 16 bis 160 Hz, von 160 bis 1600 Hz und von 1,6 kHz bis 16 kHz, dann müsste der Tieftöner, der von dem Tiefpassfilter mit einer Grenzfrequenz von 160 Hz gespeist würde bei 1600 Hz noch einen Schalldruckpegel von 10% und bei 16 kHz noch eine Schalldruckpegel von 1% betrags- und phasenrichtig wiedergeben können. Das ist in der Realität nicht möglich und würde die weitgehend ideale Summation der einzelnen Schalldruckpegel verhindern.

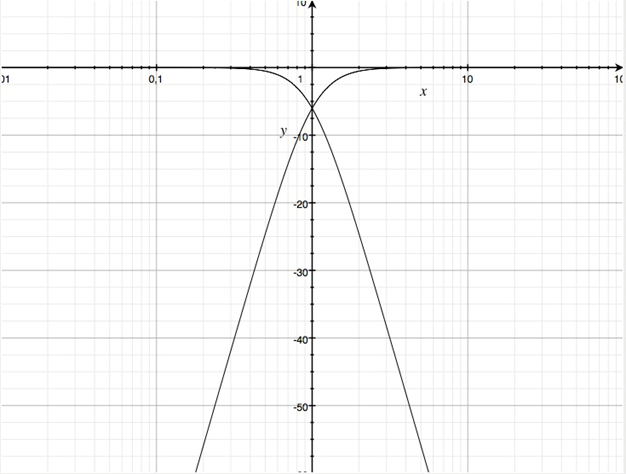
Daraus erwächst der Forderung nach größeren Flankensteilheiten des Weichenfilters, die mit höherem Grad der Übertragungsfunktion möglich werden. Das nachfolgende Bild zeigt Hochpass- und Tiefpassfilter mit 20, 40 und 60 dB/Frequenzdekade entsprechend Graden der Übertragungsfunktion von 1, 2 und 3.

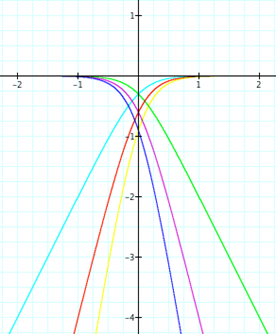
Horizontal sind Frequenzdekaden aufgetragen, vertikal der Betrag in Bel (1 B = 10 dB)

Im Fall von 60 dB/Dekade müsste also im genannten Beispiel der Tieftöner bei 1600 Hz nur noch 0,1% des Schalldruckpegels zur Summation beisteuern. Betrags- und Phasenfehler des Tieftöners spielen somit bei dieser Frequenz keine signifikante Rolle mehr. Dennoch wird aus dieser Überlegung deutlich, dass die Töner auch im benachbarten Bereich der Trennfrequenzen des Weichenfilters betrags- und phasenrichtig wandeln können müssen.

Stabilitätsbedingung von Übertragungsfunktionen

Übertragungsfunktionen für kausale Systeme müssen ihre Pole (das sind die Nullstellen des Nennerpolynoms) in der negativen komplexen p-Halbebene haben.

Eine stabile Übertragungsfunktion von Grad 2 hat die allgemeine Form

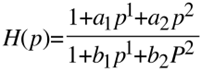
mit der Stabilitätsbedingung, dass alle Nennerkoeffizienten b_n positiv sind.

Forderung nach geometrisch symmetrischem Frequenzverhalten

Ohne unzulässige Einschränkung der Allgemeinheit kann obige Funktion normiert werden mit dem Ziel geometrisch symmetrischen Frequenzverhaltens, was bei der normierten Mittenfrequenz bezüglich der Hochachse spiegelbildliche Betragsfrequenzgänge ergibt. Diese Forderung ist nicht zwingend, aber sinnvoll.

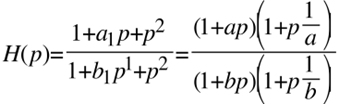
Es gelten also folgende Korrespondenzen:

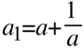
und

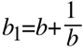
Zerlegung in Teilübertragungsfunktionen

Das Ziel der Zerlegung in Teilübertragungsfunktionen ist es eine Summenfunktion mit dem Wert 1 oder dem Betrag 1 zu bilden. Dann und nur dann entspricht das Ausgangssignal oder sein Betrag nach der Summierung dem Eingangssignal.

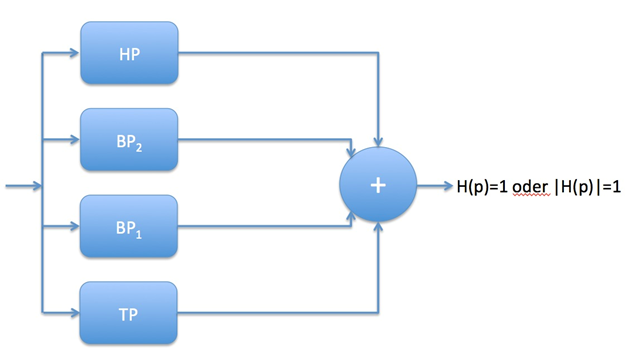
Beispiel:

Es gibt im obigen Beispiel vom Grad 2 drei Möglichkeiten Teilübertragungsfunktionen zu bilden:

1. Dreiwegweiche:

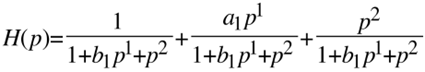
wenn man a₁ = b₁ wählt erhält man das gewünschte Ergebnis der Summation zu Eins. Allerdings ist die Flankensteilheit des Bandpassfilters (mittlerer Summand) wegen des Gradunterschieds 1 zwischen Zähler und Nenner nur 20 dB/Dekade.

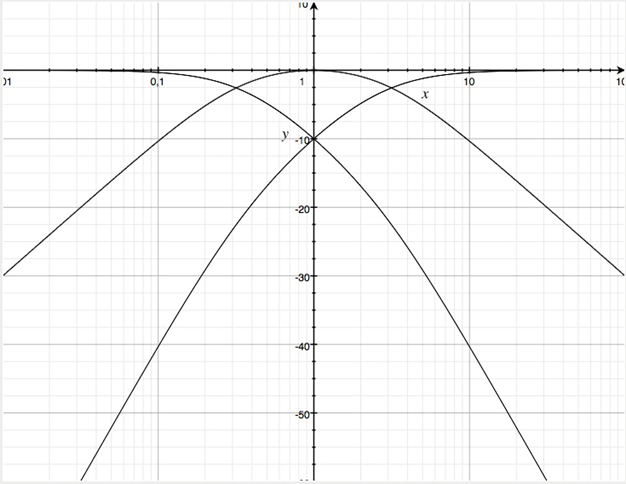
Betragsfrequenzgang in dB der Teilübertragungsfunktionen der Beispielfunktion

Der Betragsfrequenzgang in dB der Teilfilter ist für den Parameter b₁ = √10 gezeigt, was den Schnittpunkt der Betragsfrequenzgänge des HP-Filters mit dem BP-Filter bezüglich jenes des BP-Filters mit dem TP-Filter gerade eine Frequenzdekade weit festlegt.

Wenn man die Frequenzskala entnormiert multipliziert man alle normierten Frequenzen mit der geometrischen Mittenfrequenz des Audiobereiches von 16 Hz bis 16 kHz entsprechend 506 Hz. Somit ist die untere Trennfrequenz 160 Hz und die obere Trennfrequenz 1600 Hz, das gesamte Frequenzband ist also in logarithmisch äquidistante Frequenzbereiche von jeweils einer Frequenzdekade aufgeteilt.

Offensichtlich werden die maximalen Steilheiten der Filterflanken für den HP und den TP erst mit einem größeren Abstand zur jeweiligen Trennfrequenz erreicht. Für die Praxis ist die Beispielfunktion als Weichenfilter nur bedingt brauchbar, da die Steilheit der Filterflanken zu gering ist. Aus dem Diagramm ist leicht abzulesen, dass z.B. der Tieftöner bei der oberen Trennfrequenz von 1600 Hz noch -23 dB

Schalldruckpegel betrags- und phasenrichtig zur Summierung der einzelnen Schalldrücke beitragen müsste.

2. Zweiwegweiche A:

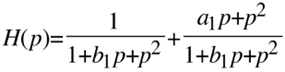
Nun hat der Tieftonkanal 40dB/Dekade (Gradunterschied von Zähler und Nenner von 2), und der Hochtonkanal zeigt 20 dB/Dekade (Gradunterschied von Zähler und Nenner von 1).

3. Zweiwegweiche B:

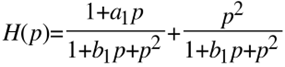
Nun hat der Tieftonkanal 20dB/Dekade (Gradunterschied von Zähler und Nenner von 1), und der Hochtonkanal zeigt nun 40 dB/Dekade (Gradunterschied von Zähler und Nenner von 2).

Diese vorgestellte Systematik von Zerlegung von Übertragungsfunktionen in entsprechende Teilübertragungsfunktionen liefert naturgemäß immer den Wert Eins (und somit Phase Null und Gruppenlaufzeit Null) der Summenübertragungsfunktion.

Alle drei beispielhaft gezeigten Zerlegungen der Übertragungsfunktion H(p) erfüllen jedoch nicht die Anforderung an ausreichende Flankensteilheiten der Teilfilter.

Will man letztere erfüllen, dann braucht man entsprechend höhere Graddifferenzen in den Teilübertragungsfunktionen, was zu einem höheren Grad der Summenübertragungsfunktion führt.

Alternativ und i.a. einfacher ist es die unerwünschten Zählersummanden zu Null zu setzen. Im obigen Beispiel würde dann a₁ = 0 gewählt werden. Dieses Verfahren bedingt allerdings allpasshaltige Summenübertragungsfunktionen.

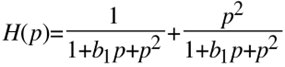
Mögliche Architekturen für Vierwegweichen

Zerlegung des Audiofrequenzbandes mit Einzelfiltern:

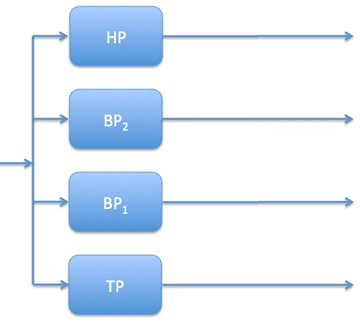
Zerlegung des Audiofrequenzbandes in einer Kaskadenstruktur:

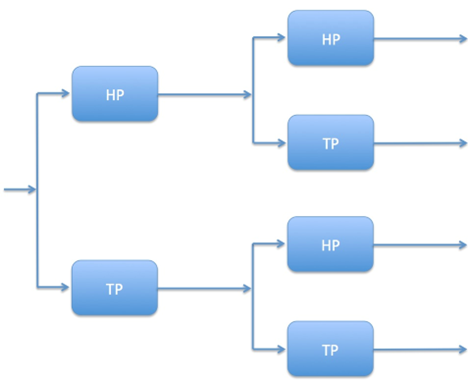
Zerlegung des Audiofrequenzbandes mit einer Dreiwegkaskade:

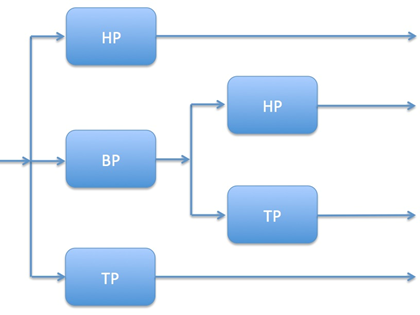
Mögliche Architekturen für Dreiwegweichen

Zerlegung des Audiofrequenzbandes via Subtraktion:

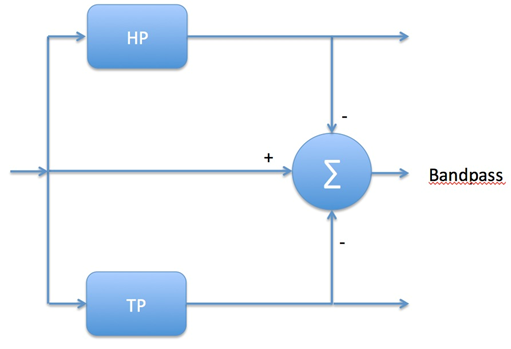
Zerlegung des Audiofrequenzbandes via Subtraktion:

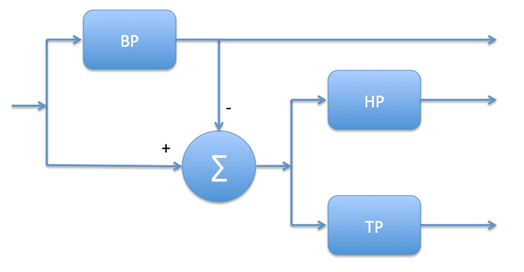
Zerlegung des Audiofrequenzbandes via Subtraktion:

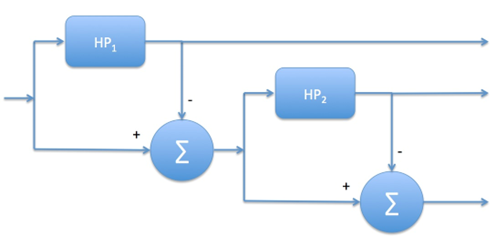
Obige Struktur ist auf beliebig viele Kanäle erweiterbar, der HP kann durch einen TP ersetzt werden.

Alle obigen Strukturen können im Falle von Weichenfiltern mit Summenübertragungsfunktion 1 direkt realisiert werden.

Verwendet man Weichenfilter mit dem Betrag der Summenübertragungsfunktion 1 dann muss die Phasendrehung der einzelnen Teilfunktionen mit entsprechenden Allpässen kompensiert werden, so dass die Summierung über Alles den Betrag 1 ergeben kann.

Übertragungsfunktion vom Grad 3

Wegen der Forderung nach geometrisch symmetrischem Frequenzverhalten lautet die Summenübertragungsfunktion

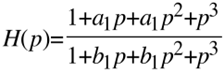
Damit die Übertragungsfunktion den Wert 1 hat muss offensichtlich gelten: a₁ = b1.

Da das Zählerpolynom ebenso wie das Nennerpolynom nur aus dem Produkt entweder reeller oder konjugier komplexer Linearfaktoren bestehen darf gilt

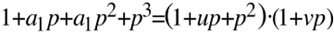
Aus dem Koeffizientenvergleich erhält man unmittelbar v=1 und b₁=u+1.

Da u und v reelle positive Koeffizienten sein müssen, wenn die Nullstellen in der negativen komplexen Halbebene liegen sollen (Stabilitätskriterium für das Nennerpolynom – nicht notwendig für das Zählerpolynom), muss also für Stabilität b₁>1 gelten.

Versucht man die gezeigte Aufteilung in Teilfunktionen erhält man für eine:

Vierwegweiche

Der Koeffizient des Linearfaktors ist zu u=2.2 gewählt, was für eine Vierwegweiche eine logarithmisch äquidistante Auftrennung in die vier Teilfrequenzbänder
16 Hz – 90 Hz – 506 Hz – 2845 – 16 kHz ergibt.

Aufgrund des Gradunterschiedes zwischen Zähler- und Nennerpolynom der Teilübertragungsfunktionen treten Flankensteilheiten von ±20, ±40 und ±60 dB/Frequenzdekade auf. Der Tief-Mitteltöner muss also einen erheblichen tieffrequenten Schallanteil, der Mittel-Hochtöner einen erheblichen hochfrequenten Schallanteil betrags- und phasenrichtig wiedergeben können.

Die Überhöhung der beiden mittleren Kanäle beträgt 0.3 dB.

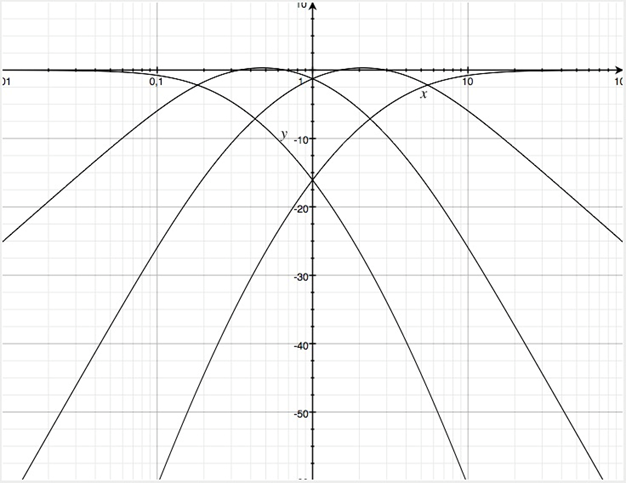
Betragsfrequenzgänge in dB der Vierwegweiche für logarithmisch äquidistante Frequenzbänder (Faktor 5,6234). Entnormierung mit 506 Hz

Dreiwegweiche

Die Betragsfrequenzgänge in dB sind für den Koeffizienten u=1.95 dargestellt, was für die Dreiwegweiche logarithmisch äquidistante Frequenzbänder ergibt.

Die Flankensteilheiten sind ±20 dB und ±60 dB. Die Überhöhung des mittleren Frequenzbandes beträgt 3.6 dB. Problematisch ist auch hier wieder der große Frequenzbereich, welchen der Mitteltöner auch außerhalb seiner Bandgrenzen von 160 Hz bis 1600 Hz betrags- und phasenrichtig verarbeiten müsste.

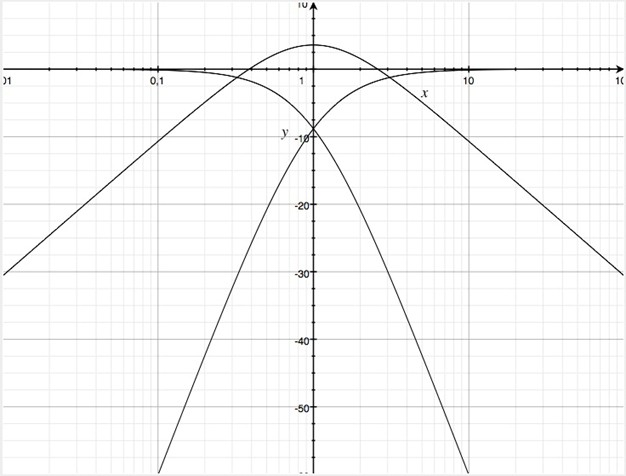
Betragsfrequenzgänge in dB für die Dreiwegweiche

Zweiwegweiche

Fasst man die Zählersummanden für eine Zweiwegweiche zusammen, so ist der Koeffizient u>0 frei wählbar. Die Betragsfrequenzgänge in dB einer Zweiwegweiche sind im Folgenden für u=1, 2, 4 gezeigt. Die Überhöhungen im Betragsfrequenzgang sind für u=1 gleich 4.5 dB, für u=2 gleich 2.2 dB und für u=4 gleich 1.2 dB. Mit wachsendem Koeffizient u wird die maximale Flankensteilheit von ±40 dB/Frequenzdekade später erreicht.

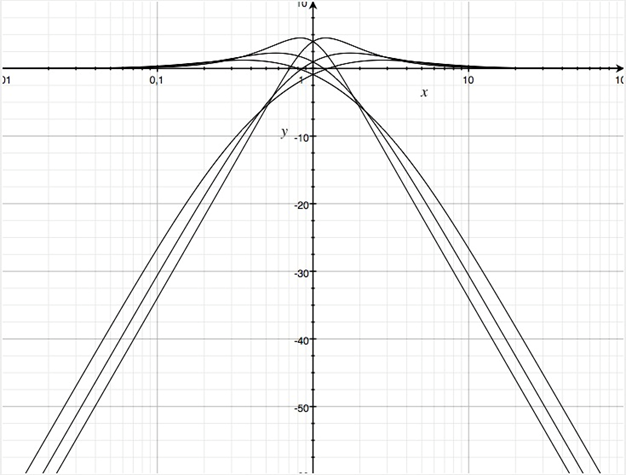
Betragsfrequenzgänge in dB der Teilfilter für den frei wählbaren Koeffizienten u = 1, 2, 4. Kleineres u hat größere Überhöhungen zur Folge

Diese Weiche könnte auch eine Dreiwegweiche mit Trennfrequenzen für ein Vierwegsystem zu einer Vierwegweiche erweitern (Kaskade zum Bandpass).

Diese Weiche könnte in einer Kaskadenstruktur zur ZeroTau Vierwegweiche erweitert werden (Beispiel nachfolgend).

Zweiwegweiche mit Allpass

Wenn man eine allpasshaltige Weiche akzeptiert, dann kann man die Zählerkoeffizienten a1=0 setzten was für u=-1 ergibt, also Nullstellen in der rechten Halbebene. Im Nenner muss aus Stabilitätsgründen u=1 gewählt werden was für b1= 2 zur Folge hat. Im Betragsfrequenzgang spielt diese Vorzeichenwahl keine Rolle, man erhält also nach-wie-vor den Betragsfrequenzgang der Summenfunktion zu Eins.

Die Betragsfrequenzgänge haben nun Flankensteilheiten von ±60 dB/Frequenzdekade und ihr Schnittpunkt liegt nun bei -3 dB. Die Summenfunktion dieser allpasshaltigen Weiche hat einen Phasenverlauf von 0 nach -360 Grad zu hohen Frequenzen.

Man erkauft also steilere Flanken mit einer Phasendrehung der Summenfunktion.

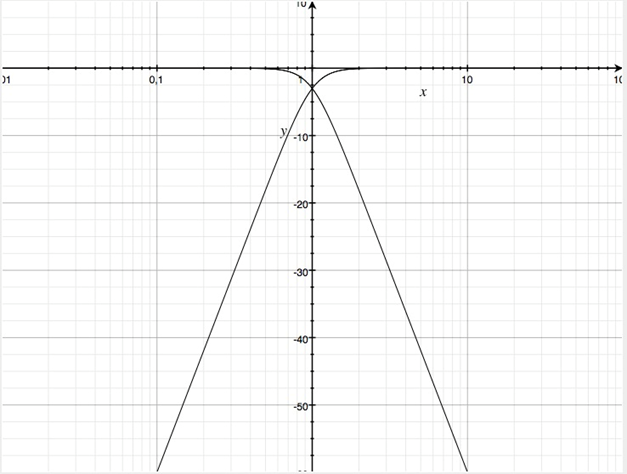
Betragsfrequenzgänge in dB der Teilfunktionen der allpasshaltigen Zweiwegweiche

Übertragungsfunktion vom Grad 4

Wegen der Forderung nach geometrisch symmetrischem Frequenzverhalten lautet die Summenübertragungsfunktion

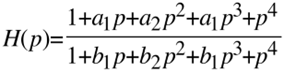
Damit die Übertragungsfunktion den Wert 1 hat muss offensichtlich gelten: a₁ = b1 und a₂=b₂.

Da das Zählerpolynom ebenso wie das Nennerpolynom nur aus dem Produkt entweder reeller oder konjugier komplexer Linearfaktoren bestehen darf gilt

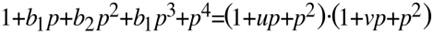
Aus dem Koeffizientenvergleich erhält man unmittelbar b₁=u+v und b₂=2+uv.

Da u und v reelle positive Koeffizienten sein müssen, wenn die Nullstellen in der negativen komplexen Halbebene liegen sollen (Stabilitätskriterium für das Nennerpolynom – nicht notwendig für das Zählerpolynom), muss also für Stabilität b₁>0 und b₂>2 gelten.

Versucht man die gezeigte Aufteilung in Teilfunktionen erhält man für eine:

Fünfwegweiche

Mit dem untenstehenden Parametersatz erhält man

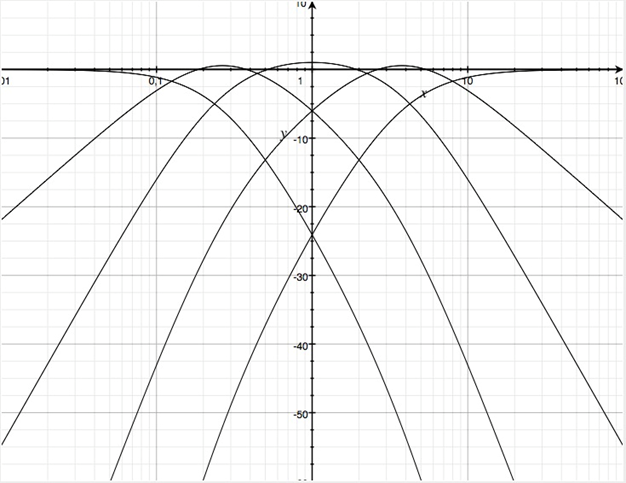
Betragsfrequenzgänge in dB der Teilfunktionen für eine Fünfwegweiche. Die Trennfrequenzen sind hier:

(16 Hz) – 63 Hz – 228 Hz – 1148 Hz – 4019 Hz – (16000 Hz)

Problematisch sind die beiden Flanken mit ±20 dB/Frequenzdekade.

Dreiwegweiche

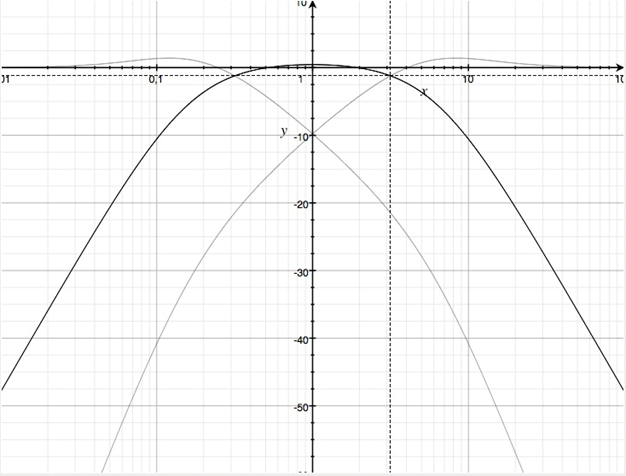
Betragsfrequenzgänge in dB der Teilfunktionen für den Koeffizienten u=v=6.2 für drei logarithmisch äquidistante Frequenzbänder

Problematisch ist der langsame Übergang der Flanken in ihre maximale Steilheit von ±40 dB/Frequenzdekade.

Dreiwegweiche mit Allpass

Lässt man eine allpasshaltige Summenübertragungsfunktion zu, so kann man den Koeffizient a₁=0 wählen, womit u=-v, a₂=2-u², b₁=u+v und b₂=2+u² wird. Für logarithmisch äquidistante Frequenzbänder wählt man u=2.8.

Die Summenübertragungsfunktion weist nun eine Phasendrehung um 270 Grad auf.

Die Überhöhung im Betragsfrequenzgang des Mittelton-Kanals beträgt 1.9 dB.

Tief- und Hochpass haben Flanken von ±60 dB, der Bandpass von ±40 dB.

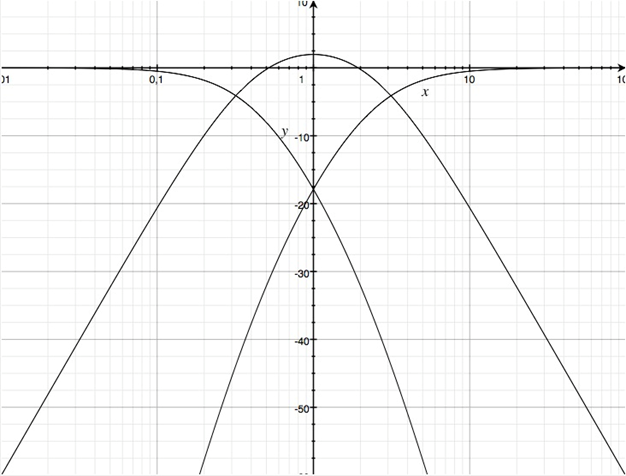
Betragsfrequenzgänge in dB der Teilübertragungsfunktionen einer Dreiwegweiche mit Allpass

Zweiwegweiche mit Allpass

Gruppiert man die Zählersummanden für eine Zweiwegweiche und lässt einen Allpass zu, so erhält man mit a₁=a₂=0 und folglich u=-v mit u=±√2. Daraus folgt b₁= 2√2 und b₂=4.

Betragsfrequenzgänge einer Zweiwegweiche mit Allpass

Die Flankensteilheut beträgt nun ±80 dB/Frequenzdekade und der Schnittpunkt bei der Trennfrequenz liegt bei -6 dB.

Der Summenfrequenzgang dreht die Phase um 360 Grad.

Beide Filterausgänge haben identischen Phasenwinkel der identisch zur Summenfunktion ist.

Übertragungsfunktion vom Grad 5

Wegen der Forderung nach geometrisch symmetrischem Frequenzverhalten lautet die Summenübertragungsfunktion

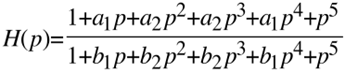
Damit die Übertragungsfunktion den Wert 1 hat muss offensichtlich gelten: a₁ = b₁ und a₂=b₂.

Da das Zählerpolynom ebenso wie das Nennerpolynom nur aus dem Produkt entweder reeller oder konjugier komplexer Linearfaktoren bestehen darf gilt

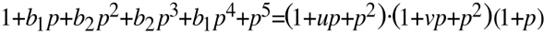
Aus dem Koeffizientenvergleich erhält man unmittelbar b₁=1+u+v und b₂=b₁+1+uv.
Da u und v reelle positive Koeffizienten sein müssen, wenn die Nullstellen in der negativen komplexen Halbebene liegen sollen (Stabilitätskriterium für das Nennerpolynom – nicht notwendig für das Zählerpolynom), muss also für Stabilität b₁>1 und b₂>2 gelten.
Versucht man die gezeigte Aufteilung in Teilfunktionen erhält man für eine:

Vierwegweiche

Mit a₁=b₁ und a₂=b₂ und u=v=10 erhält man vier logarithmisch äquidistante Frequenzbänder. Die Koeffizienten u und v können jedoch auch unabhängig voneinander gewählt werden.

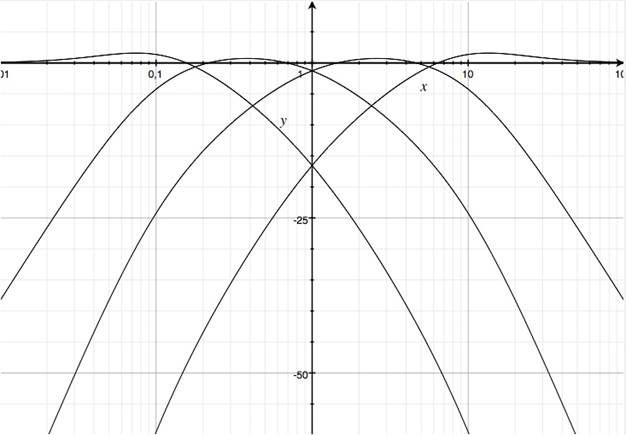
Betragsfrequenzgänge in dB einer Vierwegweiche

Vierwegweiche mit Allpass

Setzt man den Koeffizienten a₁=0 entsteht eine allpasshaltige Summenübertragungsfunktion.

Mit u=4.7, v=u, b₁=1+u+v, b₂=1+b₁+uv, a₁=0 und a₂=2+u+(-1-u)+u(-1-u) erhält man die dargestellten Betragsfrequenzgänge.

Die Hochpass- und Tiefpassübertragungsfunktion weist nun höhere Flankensteilheit von ±60 dB/Frequenzdekade auf.

Problematisch und unverändert könnte die Flankensteilheit des Tief-Mitteltonkanales sein, der zunächst nur mit 30 dB/Frequenzdekade abfällt. Spiegelsymmetrisch zur Hochachse verhält sich der Mittel-Hochtonkanal.

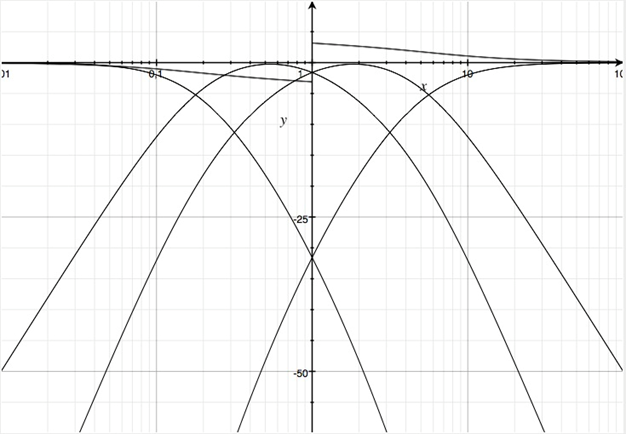
Betragsfrequenzgänge in dB einer Vierwegweiche mit Allpasscharakteristik

Dreiwegweiche

Gruppiert man die Zählersummanden für eine Dreiwegweiche erhält man mit a₁=b₁ und a₂=b₂ und u=v=4.7

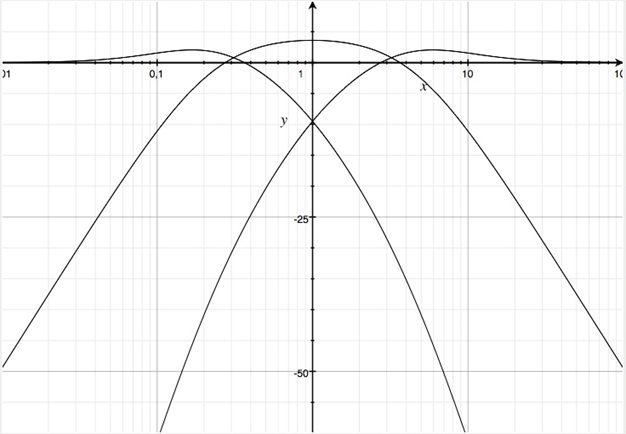
Betragsfrequenzgänge in dB der Teilübertragungsfunktionen einer Dreiwegweiche

Dreiwegweiche mit Allpass

Setz man zusätzlich den Koeffizienten a₁=0, so erhält man mit u=v=2.8 eine allpasshaltige Übertragungsfunktion, welche die Phase um 360 Grad dreht.

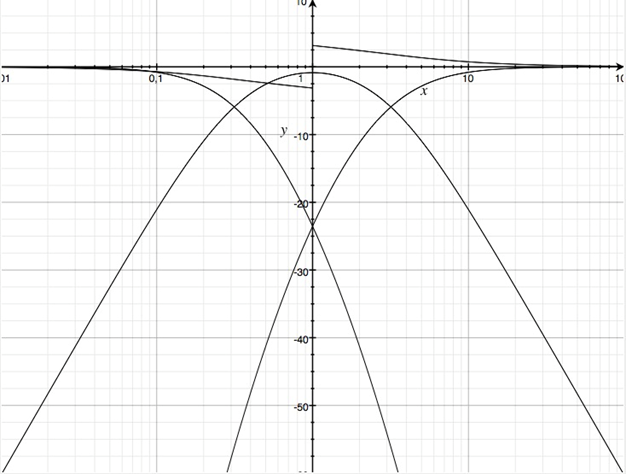
Betragsfrequenzgänge in dB der Teilübertragungsfunktionen einer Dreiwegweiche mit Allpasscharakter

Zweiwegweiche

Wählt man u=v=3 und a₁=b₁ und a₂=b₂, so erhält man mit entsprechender Gruppierung der Zählersummanden eine Zweiwegweiche mit einer anfänglichen Flankensteilheit von ±40 dB/Frequenzdekade, die dann auf ±60 dB/Frequenzdekade ansteigt.

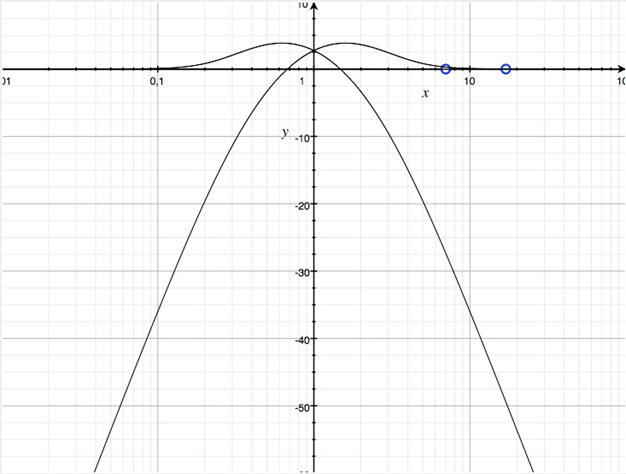
Betragsfrequenzgänge der Teilfunktionen einer Zweiwegweiche

Problematisch die Überhöhung von ca. 4 dB.

Diese Weiche könnte in einer Kaskadenstruktur zur ZeroTau Vierwegweiche erweitert werden.

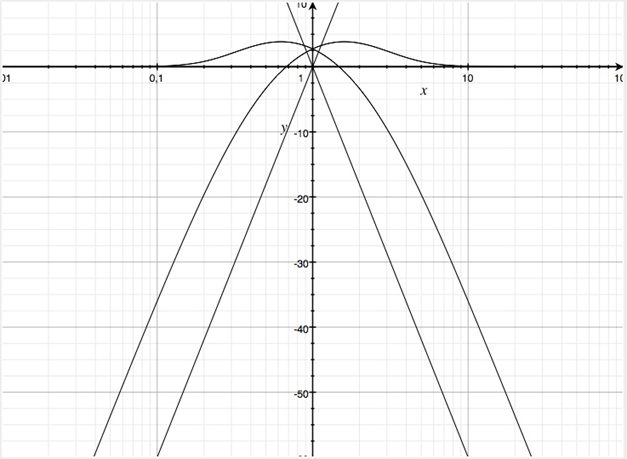
Betragsfrequenzgänge in dB der Teilfunktionen der obigen Zweiwegweiche mit Geraden der Steigung ±60 dB/Frequenzdekade

Zweiwegweiche mit Allpasscharkter

Setzt man a₁=a₂=0 erhält man mit u=-1/2+1/2√5 und v= +1/2+1/2√5 eine Zweiwegweiche deren Summenfunktion die Phase um 360 Grad dreht. Die Flankensteilheit ist nun ±100 dB/Frequenzdekade.

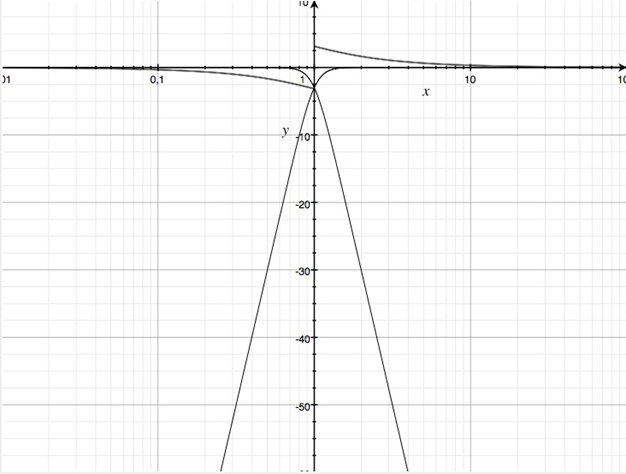
Betragsfrequenzgänge der Teilfunktionen einer Zweiwegweiche mit Allpasscharakter

Bei dieser Weiche sind die Teilfunktionen konstant um 90 Grad gegeneinander verschoben, der Schnittpunkt liegt somit bei -3 dB.

Übertragungsfunktion vom Grad 6

Wegen der Forderung nach geometrisch symmetrischem Frequenzverhalten lautet die Summenübertragungsfunktion

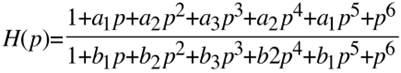
Damit die Übertragungsfunktion den Wert 1 hat muss offensichtlich gelten: a₁ = b₁, a₂=b₂ und a₃=b₃.

Da das Zählerpolynom ebenso wie das Nennerpolynom nur aus dem Produkt entweder reeller oder konjugier komplexer Linearfaktoren bestehen darf gilt

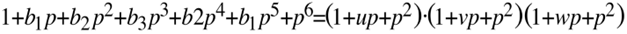
Aus dem Koeffizientenvergleich erhält man unmittelbar b₁=u+v+w, b₂=3+uv+uw+vw und b₃=2(u+v+w)+uvw.

Da u, v und w reelle positive Koeffizienten sein müssen, wenn die Nullstellen in der negativen komplexen Halbebene liegen sollen (Stabilitätskriterium für das Nennerpolynom – nicht notwendig für das Zählerpolynom), muss also für Stabilität b₁>0 b₂>3 und b₃>2 gelten.

Versucht man die gezeigte Aufteilung in Teilfunktionen erhält man für eine:

Dreiwegweiche

Mit u=v=w=9 erhält man eine Dreiwegweiche mit logarithmisch äquidistanten Frequenzbändern

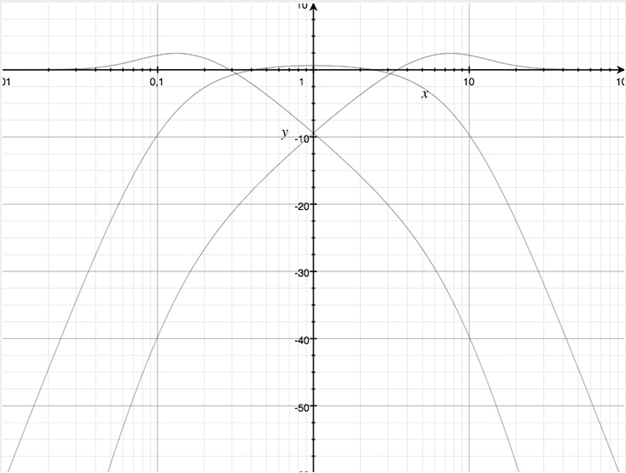
Betragsfrequenzgänge in dB der Teilfunktionen einer Dreiwegweiche

Dreiwegweiche mit Allpasscharakteristik

Setzt man a₁=a₂=0 erhält man Gleichungen, welche wegen der Diskriminante v≤2 bedingen. Damit lassen sich die Trennfrequenzen nicht wie erforderlich einstellen.

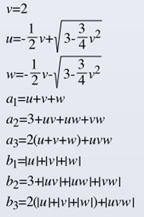
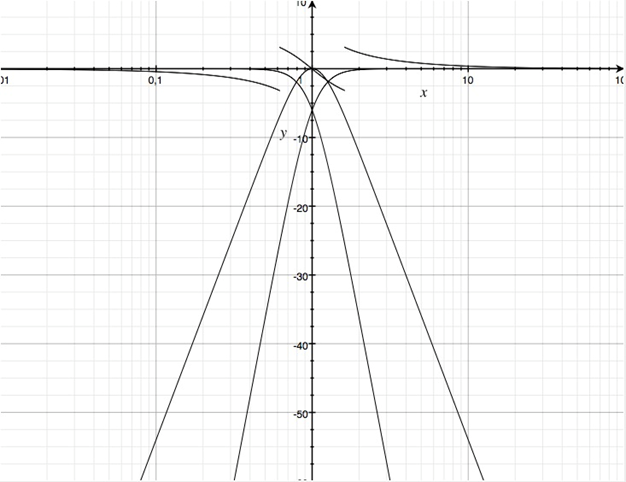
Betragsfrequenzgänge in dB der Teilfunktionen einer Dreiwegweiche mit Allpasscharkter

Vierwegweiche mit Allpasscharakteristik

Der naheliegende Gedanke eine Vierwegweiche mit a₁=0 und a3=0 zu bilden ist nicht durchführbar, da wegen a₁=u+v+w, und a₃=2(u+v+w)+uvw folgen würde, dass uvw=0 sei. Das verletzte die Forderung nach u, v, w>0.

Übertragungsfunktion vom Grad 7

Wegen der Forderung nach geometrisch symmetrischem Frequenzverhalten lautet die Summenübertragungsfunktion

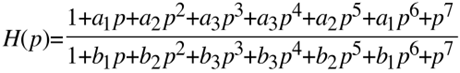
Damit die Übertragungsfunktion den Wert 1 hat muss offensichtlich gelten: a₁ = b₁, a₂=b₂ und a₃=b₃.

Da das Zählerpolynom ebenso wie das Nennerpolynom nur aus dem Produkt entweder reeller oder konjugier komplexer Linearfaktoren bestehen darf gilt

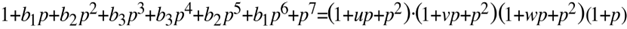
Aus dem Koeffizientenvergleich erhält man unmittelbar

b₁=1+u+v+w,

b₂=2+u+v+w+uv+uw+vw+uvw und

b₃=3+2(u+v+w)+uv+uw+vw+uvw.

Da u, v und w reelle positive Koeffizienten sein müssen, wenn die Nullstellen in der negativen komplexen Halbebene liegen sollen (Stabilitätskriterium für das Nennerpolynom – nicht notwendig für das Zählerpolynom), muss also für Stabilität
b₁>1, b₂>2 und b₃>3 gelten.

Versucht man die gezeigte Aufteilung in Teilfunktionen erhält man für eine:

Vierwegweiche

Mit dem untenstehenden Parametersatz erhält man

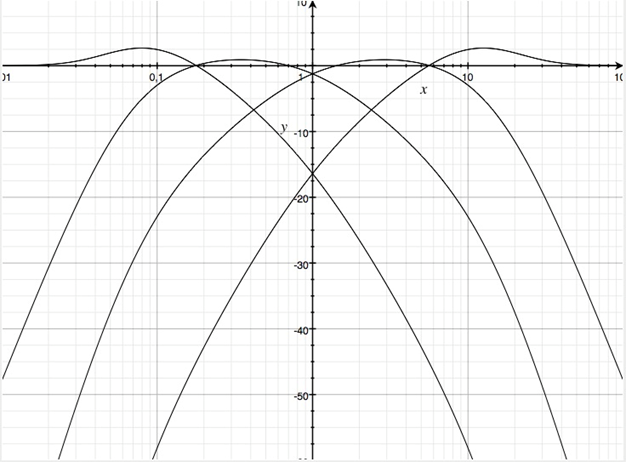
Betragsfrequenzgänge in dB der Teilfunktionen einer Vierwegweiche

Die Überhöhungen in den Betragsfrequenzgängen beträgt weniger als 2.5 dB.

Vierwegweiche mit Allpasscharakteristik A

Lässt man allpasshaltige Funktionen zu, kann man a₂=0 setzen und erhält mit dem Parametersatz

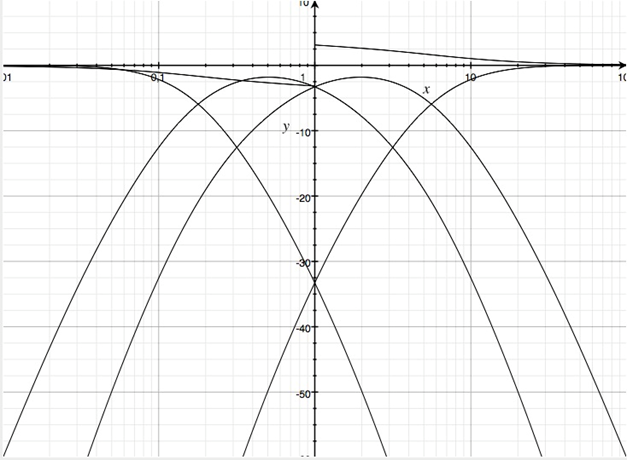
Betragsfrequenzgänge in dB der Teilfunktionen einer Vierwegweiche mit Allpasscharkter

Die Summenfunktion dreht die Phase um 360 Grad.

Vierwegweiche mit Allpasscharakteristik B

Setzt man beide Koeffizienten a₁=a₂=0 erhält man

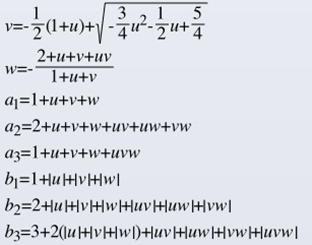
was für u<-1.6 zu negativer Diskriminante führt und somit die Trennfrequenzen nicht wie gefordert einstellen lässt.

Dreiwegweiche

Mit dem untenstehenden Parametersatz erhält man

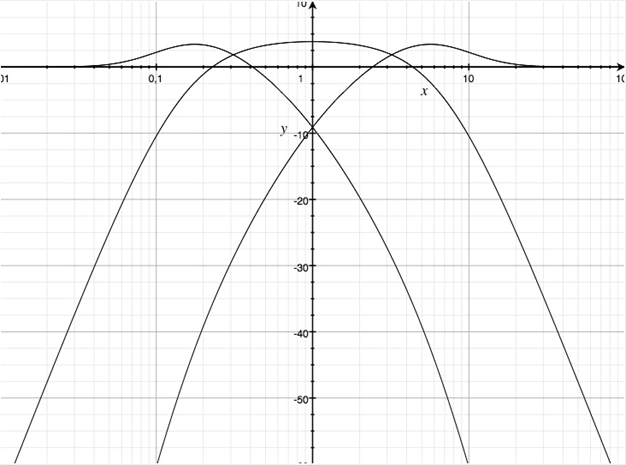
Betragsfrequenzgänge in dB der Teilfunktionen einer Dreiwegweiche

Zweiwegweiche

Mit dem untenstehenden Parametersatz erhält man

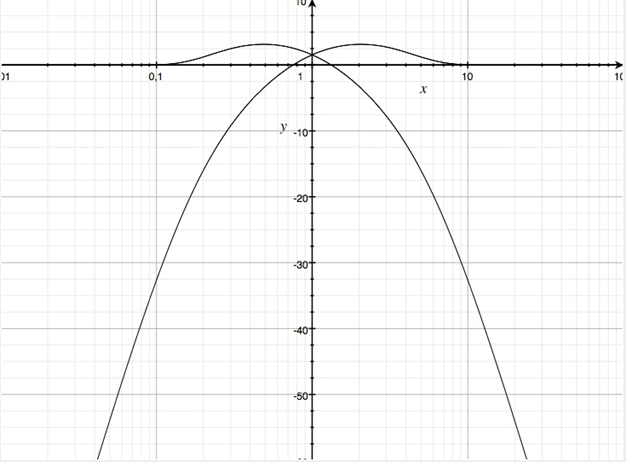
Betragsfrequenzgänge in dB der Teilfunktionen einer Zweiwegweiche

Die Betragsüberhöhung ist in der gewählten Dimensionierung 3 dB.

Zum Vergleich sind zusätzlich die Steigungen ±80 dB/Frequenzdekade eingezeichnet

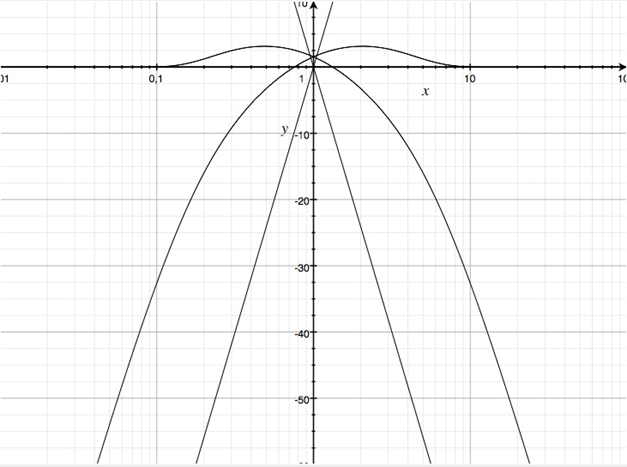
Betragsfrequenzgänge in dB der Teilfunktionen einer Zweiwegweiche mit Geraden der Steigungen ±80 dB/Frequenzdekade

Übertragungsfunktion vom Grad 7

Wegen der Forderung nach geometrisch symmetrischem Frequenzverhalten lautet die Summenübertragungsfunktion

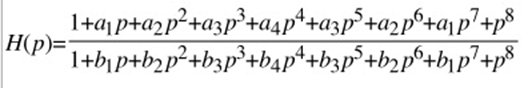
mit vier Linearfaktoren:

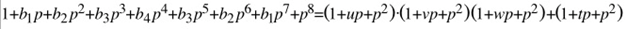
Damit die Übertragungsfunktion den Wert 1 hat muss offensichtlich gelten: a₁ = b₁, a₂=b₂, a₃=b₃ unda₄=b₄.

Aus dem Koeffizientenvergleich erhält man unmittelbar

Da u, v, w und t reelle positive Koeffizienten sein müssen, wenn die Nullstellen in der negativen komplexen Halbebene liegen sollen (Stabilitätskriterium für das Nennerpolynom – nicht notwendig für das Zählerpolynom), muss also für Stabilität
b₁>0, b₂>4, b₃>0 und b₄>6 gelten.

Versucht man die gezeigte Aufteilung in Teilfunktionen erhält man für eine:

Dreiwegweiche

Dreiwegweiche mit Allpasscharakteristik

Koeffizient a₂=0

Betrachtung zur Phasenlage der Teilsignale dieser Weichenklassen

Die Besonderheit der vorgestellten Weichenfilter besteht darin, dass sie entweder die Summenfunktion Eins haben oder diese, falls allpasshaltig zumindest den Betrag Eins hat. Daraus folgt dies auch unmittelbar für die Summe der Vektoren der Teilsignale bei jeder Frequenz: Die Vektoren der Teilsignale summieren sich zum Wert Eins (im Bild dargestellt), oder zum Betrag eins (Vektor der Länge Eins, aber beliebiger Phase).

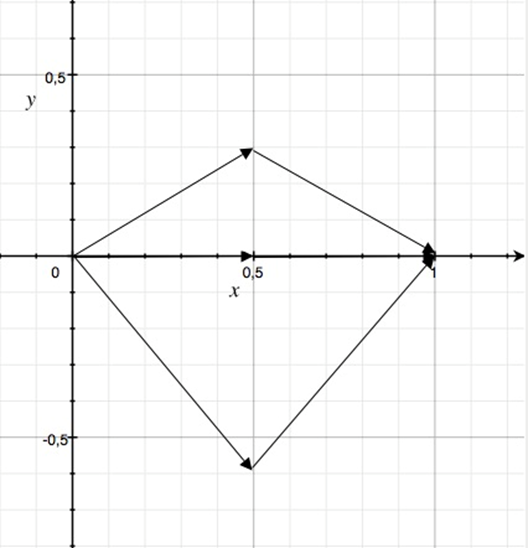
Dabei können die Teilvektoren unterschiedliche Phasenlage aufweisen. Je stärker die Teilvektoren von der Phase 0 Gad abweichen, umso größer ist die Überhöhung des Betragsverlaufes der korrespondierenden Frequenzgänge bezogen auf ½ bzw. -6 dB. Nur beim Grad 4 existiert ein allpasshaltiges Filter bei welchem alle Teilvektoren die Phasenlage 0 Grad aufweisen. Damit müssen sich die Betragsfrequenzgänge bei ½ bzw. -6 dB schneiden. Im Bild ist das am mittleren Beispiel veranschaulicht. Überhöhungen größer als 0 dB bei den Trennfrequenzen kommen durch Teilvektoren zustande, die gegeneinander mehr als 120 Grad in der Phase verschoben sind.

Entnormierung und logarithmisch äquidistante Frequenzbänder

Nimmt man den hörbaren Frequenzbereich zu 16 Hz bis 16000 Hz an, so sind diese beiden Frequenzgrenzen um eine Faktor 1000 separiert.

Die geometrische Mitte des Frequenzbandes ist dann √(16*16000) = 506 Hz.

Alle auf die Mittenfrequenz 1 normierten Frequenzen müssen zum Entnormieren mit 506 Hz multipliziert werden.

Bei einer Dreiwegweiche will man drei logarithmisch äquidistante Frequenzbänder erzeugen. Dazu müssen die Trennfrequenzen um einen Faktor 1000^1/3 = 10 separiert sein. Somit erhält man die Trennfrequenzen:

16Hz – 160 Hz – 1600 Hz – 1600 Hz

Bei einer Vierwegweiche will man vier logarithmisch äquidistante Frequenzbänder erzeugen. Dazu müssen die Trennfrequenzen um einen Faktor 1000^1/4 = 5.623 separiert sein. Somit erhält man die Trennfrequenzen:

16Hz – 90 Hz – 506 Hz – 2845 Hz – 1600 Hz

Bei einer Fünfwegweiche will man fünf logarithmisch äquidistante Frequenzbänder erzeugen. Dazu müssen die Trennfrequenzen um einen Faktor 1000^1/5 = 3.981 separiert sein. Somit erhält man die Trennfrequenzen:

16Hz – 64 Hz – 253 Hz – 1009 Hz – 4019 Hz – 1600 Hz