Phase Modulation of Loudspeakers

What is it about?

The membrane of a loudspeaker travels at low frequencies considerable distances back and forth. In the following example the distance change is assumed to be ±7 mm from the rest position.
The human eardrum, or the membrane of the condenser microphone used for the recording travel negligible distances of about 1 µm @ 25 Hz and 100 dB SPL.

This factor of about 10000 between the travel amplitudes of the membranes (and the attached air molecules) between recording and play back leads to an undesired Phase Modulation (PM) also known as Doppler Distortion, or Doppler Effect of the Sound Pressure at any distance from the source.

Thought experiment:

One can imagine a high note being played back by the loudspeaker. Simultaneously a low note with considerable membrane travel is being played back. The location at which the high note is generated travels with the membrane back and forth. Because of that the sound needs different times to arrive at the receiver. Such different membrane positions s(t) translates for each frequency to different phases at the receiver, as described by the below formula.

This principle is a general one, described by the formula below and is valid for any note or frequency, even, when only one frequency is played back.

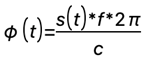
Obviously, the phase of the sound pressure is proportional to the membrane travel distance s(t) and to the frequency f considered. The speed c of the sound is 343 m/s under normal conditions.

Detailed consideration

The effect of modulating the phase of a signal is well known. The resulting spectrum is mathematically described by the Bessel functions. For the listener it has the consequence that spectral lines are generated and added to the original sound / to the original spectrum.

How does this look like in the time domain for a single frequency?

The following figure shows red the resulting SPL at the receiver for a 25 Hz frequency with 7 mm membrane travel amplitude. There is according to the Phase Modulation of the moving membrane an additional frequency visible at the receiver green (10 times magnified).

X axis: Time in Seconds, Y axis: SPL in arbitrary sound pressure units:

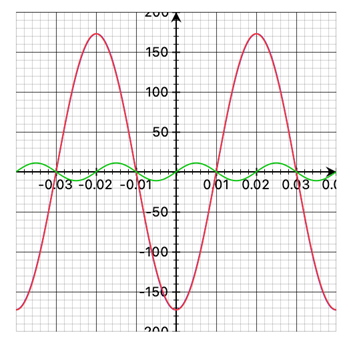
Obviously, this additional waveform has twice the frequency of the original frequency and is phase shifted by 90 degrees. The Fourier Transformation of the wave form at the receiver shows that there are further harmonic frequencies with smaller amplitudes generated.

X axis: Frequency in Hz, Y axis: SPL in dB

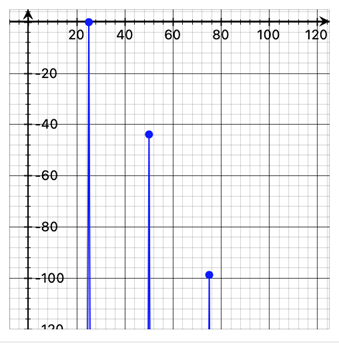
The above figure shows a second harmonics at about -44 dB with respect to the fundamental frequency. From manufacturers of loudspeaker boxes one can often hear that a harmonic distortion is not a big issue, as all music instruments generate harmonic frequencies too. However, in case there are two or more frequencies intermodulation (mixing) products are simultaneously generated, which are not harmonics to the fundamental frequency and are such extremely disturbing for a good listening experience.

The figure below shows blue the intermodulation products generated by two frequencies, the first being as before 25 Hz with 7 mm membrane travel amplitude and the second one being 1000 Hz at the same SPL as the first one. The red dots indicate the phase of the additional special lines (± 90 degrees). The largest two Bessel Lines to the fundamental frequency of 1000 Hz have about -24 dB with respect to its amplitude. Their frequency is 1000 Hz ±25 Hz. Further spectral lines appear at 1000 Hz ±n times 25 Hz (n is an integer number).

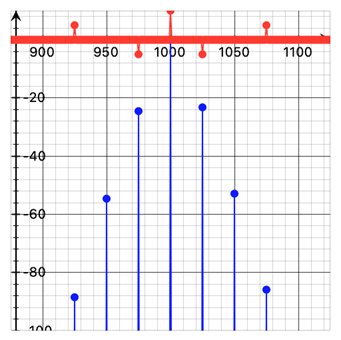
The above spectrum would be the case for a two-way loudspeaker system with a cross over frequency of 1000 Hz reproducing the two tones as in the example. The only way to get rid of these very disturbing intermodulation frequencies is using a virtual steady membrane. AudioChiemgau developed a Digital Audio Processor to eliminate the Doppler effect / the Phase Modulation by the above-mentioned technology.

Consequences for the near field measurement of loudspeakers

The second harmonics in the above example is 44 dB below the fundamental frequency of 25 Hz.

Even when for a measurement of the linearity of a chassis or its harmonic distortions the Nonlinear Amplitude Modulation is compensated, there remains the limit though the Phase Modulation.

Other than for the Nonlinear Amplitude Modulation the Phase Modulation is independent from the distance to the measurement microphone. In the above case the measurement dynamics would be limited to about 44 dB for the second harmonics of the 25 Hz spectral line.

In case of two-tone measurements, one would get the Doppler (a.k.a. Bessel) spectral lines as above.
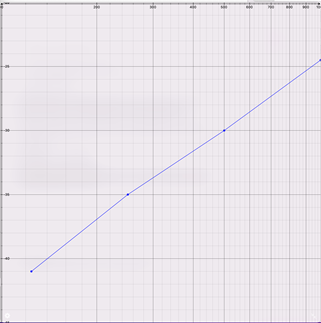
The figure below shows the SPL amplitudes of the largest Doppler Lines below the SPL of the second fundamental frequency of 1000 Hz as function of the second frequency.

As follows from the formula on the first page, the Doppler line amplitudes are proportional to the second frequency, as the phase variation of the second frequency is proportional to the total membrane excursion.

The Doppler line amplitudes are proportional to the total membrane excursion amplitude.

The Doppler amplitudes are independent from the measurement microphone (listener) distance

The figure below shows the linear increasing Doppler amplitudes versus the second frequency. It is obvious that the same membrane travel generates a phase modulation proportional to the frequency considered.

X axis: Second frequency in Hz, first frequency = 25 Hz @ 7 mm membrane travel amplitude
Y axis: SPL in dB of Doppler Line amplitude w.r.t SPL of second fundamental frequency amplitude.

Consequences for listening

The above example demonstrates that non-linearities of electro-acoustical transducers are severely disturbing a good listening experience. Additionally the Phase Modulation due to the membrane movement generates harmonic and non-harmonic spectral lines. Non-harmonic special lines are much more perceived than harmonic spectral lines. In so far any non-linearity, but also the Doppler effect has to be avoided for a good reproduction of acoustical content.

There is a paper available on the AudioChiemgau web page demonstrating how distortions from the chassis, and physical effects as the Nonlinear Amplitude Modulation and the Phase Modulation effect the transparency of the sound reproduction.

Elimination of the PM / the Doppler Effect

As the generation of the PM / Doppler effect is a physical effect, it can be compensated at any listening distance. The elimination is based on a phase modulator in a Digital Audio Processor using the membrane travel as control signal. Such it is possible to compensate (eliminate) the PM. This requires, however, the exact knowledge of the membrane position at any point in time.

AudioChiemgau offers all electronic modules for building High-End motion feedback loudspeakers and Audio Processors which can eliminate both, the Doppler effect of the moving loudspeaker membrane as well as the simultaneous generated NLAM.

All measurments are done with our ModeCompensator